Surface area to volume ratio
05/15/2013 by jgluvna
More than 250 million years ago, during the Paleozoic Era, you could find dragonflies with hawk-sized wing spans and millipedes longer than a human leg. Why do we no longer see giant bugs? This size limitation is also true for single celled organisms, like dinoflagellates and amoeba. Why do giant cells not exist? Create a model that accurately describes this problem.
As a simple example, imagine a cell shaped like a cube, with each side having length 
. This geometry means that each face of the cube has area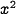 
, and since there are 6 faces, its total surface area is 
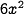. Its volume is 
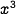. The ratio of surface area to volume is 
.
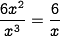Now double the size of each side to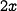 
. Now each face of the cube has area 
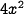, and since there are 6 faces, its total surface area is 
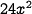. Its volume is 
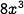. Its surface:volume ratio is 
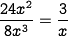. By doubling the length of each side of the cube, we have changed the surface:volume ratio by halving it. Since cells depend on taking up materials that collide with their surface, this larger cell now has a reduced ability to acquire molecules from its surroundings. A similar problem affects insects, which depend on passive diffusion to take up oxygen.
If you change the geometry from a cube to something more realistic, you will find that the math changes but the problem is fundamentally the same: making a spherical (for example) cell larger will reduce the surface:volume ratio.
Other allometry problems are also interesting, but some can be more complicated. If you were suddenly twice your size in all dimensions, would your legs be strong enough to support you?
Theory
- Allometric growth (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 366)
- Diffusion (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 552)
References
- MSNBC Article – Why today’s bugs aren’t giant?
- Niklas, Karl. (1994). Plant allometry. Chicago: University of Chicago Press.
- Calder, W. A. (1984). Size, function and life history. Cambridge, Mass.: Harvard University Press.
- McMahon, T. A. and J. T. Bonner (1983). On Size and Life. New York: Scientific American Library.
- Niklas, K. J. (1994). Plant allometry: The scaling of form and process. Chicago: University of Chicago Press.
- Peters, R. H. (1983). The ecological implications of body size. Cambridge: Cambridge University Press.
- Schmidt-Nielsen, K. (1984). Scaling: why is animal size so important?. Cambridge: Cambridge University Press.
- Samaras, Thomas T. (2007). Human body size and the laws of scaling: physiological, performance, growth, longevity and ecological ramifications.