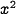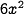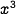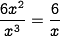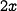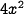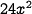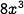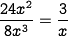STEP@USF

Welcome to the new site for the NSF-funded STEP program at the University of South Florida! This website is still under construction. However, please refer to the links section for more information. This post will remain at the top of the page, but below are some recent posts and project ideas.

Please click the link below for more information

Draining of a storage tank 

This paper will examine a series of differential equations to observe population patterns of beluga whales.

Theory

• logistic equation (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 364-366)

References

More than 250 million years ago, during the Paleozoic Era, you could find dragonflies with hawk-sized wing spans and millipedes longer than a human leg. Why do we no longer see giant bugs? This size limitation is also true for single celled organisms, like dinoflagellates and amoeba. Why do giant cells not exist? Create a model that accurately describes this problem.

As a simple example, imagine a cell shaped like a cube, with each side having length . This geometry means that each face of the cube has area 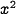, and since there are 6 faces, its total surface area is 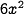. Its volume is 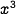. The ratio of surface area to volume is .

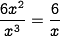Now double the size of each side to 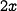. Now each face of the cube has area 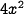, and since there are 6 faces, its total surface area is 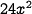. Its volume is 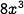. Its surface:volume ratio is 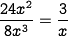. By doubling the length of each side of the cube, we have changed the surface:volume ratio by halving it. Since cells depend on taking up materials that collide with their surface, this larger cell now has a reduced ability to acquire molecules from its surroundings. A similar problem affects insects, which depend on passive diffusion to take up oxygen.

If you change the geometry from a cube to something more realistic, you will find that the math changes but the problem is fundamentally the same: making a spherical (for example) cell larger will reduce the surface:volume ratio.

Other allometry problems are also interesting, but some can be more complicated. If you were suddenly twice your size in all dimensions, would your legs be strong enough to support you?

Theory

• Allometric growth (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 366)
• Diffusion (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 552)

References

• MSNBC Article – Why today’s bugs aren’t giant?
• Niklas, Karl. (1994). Plant allometry. Chicago: University of Chicago Press.
• Calder, W. A. (1984). Size, function and life history. Cambridge, Mass.: Harvard University Press.
• McMahon, T. A. and J. T. Bonner (1983). On Size and Life. New York: Scientific American Library.
• Niklas, K. J. (1994). Plant allometry: The scaling of form and process. Chicago: University of Chicago Press.
• Peters, R. H. (1983). The ecological implications of body size. Cambridge: Cambridge University Press.
• Schmidt-Nielsen, K. (1984). Scaling: why is animal size so important?. Cambridge: Cambridge University Press.
• Samaras, Thomas T. (2007). Human body size and the laws of scaling: physiological, performance, growth, longevity and ecological ramifications.

It is believed that more than one environmental factor (total N, total P, salinity, and turbidity) is having a negative effect on seagrass coverage in Tampa Bay. Create an equation/model that predicts how the coverage of seagrass in Tampa Bay will be affected by an increase of at least two of the environmental factors (total N, total P, salinity, and turbidity) measured.

Theory

• Partial derivatives (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 526)
• Functions of two or more variables (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 526)
• Chain rule for functions of two variables (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 543)

References

The Kermack and McKendrick model (1927; 1932; 1933) or SIR model can be used to describe the progress of an epidemic through a population. The S term stands for susceptible individuals, I stands for infectious individuals (those who are infected an who can transmit the disease), and R stands for those who are recovered and now immune to the disease. Determine the number of infected individuals needed for there to be an epidemic. What happens to the progress of the epidemic when you change the number of S or R individuals? What about in populations with and without vaccinations?

Theory

• Compartment models (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 587; Stephen P. and John Guckenheimer. Dynamic Models in Biology. New Jersey: Princeton University Press, 2006. 7)
• Simple epidemic model (Neuhauser, Claudia. Calculus for Biology and Medicine. New Jersey: Prentice Hall, 2000. 387)
• Differential equation models for infectious disease (Stephen P. and John Guckenheimer. Dynamic Models in Biology. New Jersey: Princeton University Press, 2006. 183)

References